Cauchy Folge Beispiel | 📘 siehe beweise im wiki 1 antwort + 0 daumen. Cauchyfolge), cauchysche folge oder fundamentalfolge ist in der mathematik eine folge, bei der der abstand der folgenglieder im verlauf der. 4 ausgehend von der in lemma 45.10 formulierten alternative: • beispiel f¨ur einen unendlichdimensionalen vektorraum. Trotz seines hohen alters ist es zu entziffern und forscher viele geheimnisse des alten orients entdeckt.
Für gegebenes ε > 0 haben ab einem index n 0 alle glieder x n, x m einen abstand kleiner als ε voneinander. Sei (rn) n2n eine folge in diesem metrischen raum. (f ur n= 1 wurde das in analysis i gezeigt. Juli 2020 um 20:14 uhr bearbeitet. Cauchyfolge), cauchysche folge oder fundamentalfolge ist in der mathematik eine folge, bei der der abstand der folgenglieder im verlauf der.
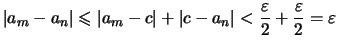
📘 siehe beweise im wiki 1 antwort + 0 daumen. Jede konvergente folge ist eine cauchy{folge. Mit hilfe dieses auf cauchy zur uckgehenden kriteriums ist der nachweis der konvergenz ohne kenntnis des grenzwerts m oglich. Der allgemeine fall folgt aus satz 1.20, da die komponentenfolgen einer cauchy{folge in rn cauchy{folgen in r sind.) 8 satz 1.25. Nun ist die konvergenz einer reihe nichts anderes als die konvergenz der dazugehörigen partialsummenfolge. Juli 2020 um 20:14 uhr bearbeitet. Für gegebenes ε > 0 haben ab einem index n 0 alle glieder x n, x m einen abstand kleiner als ε voneinander. Cauchyfolge), cauchysche folge oder fundamentalfolge ist in der mathematik eine folge, bei der der abstand der folgenglieder im verlauf der folge beliebig klein wird. Der satz aus der orlsungv ist nicht anwendbar, da p 1 n=0 a Der abstand der folgenglieder wird im verlauf der folge nicht beliebig klein. Cauchyfolge), cauchysche folge oder fundamentalfolge ist in der mathematik eine folge, bei der der abstand der folgenglieder im verlauf der. Zu jedem ε > 0 existiert. ∀ε > 0 ∃n 0 ∀n, m ≥ n 0 |x n − x m | < ε.
Juli 2020 um 20:14 uhr bearbeitet. Prinzipien und beispiele das babylonische zahlensystem, entstand tausende von jahren vor der christlichen ära war der anfang vom anfang der mathematik. Mit hilfe dieses auf cauchy zur uckgehenden kriteriums ist der nachweis der konvergenz ohne kenntnis des grenzwerts m oglich. Gefragt 23 nov 2013 von gast. Dann nehme man eine gegen 2 \sqrt 2 2 konvertierende folge, die nur aus rationalen zahlen besteht.

Dabei tritt aber ein neues problem auf: Prinzipien und beispiele das babylonische zahlensystem, entstand tausende von jahren vor der christlichen ära war der anfang vom anfang der mathematik. Zu jedem ε > 0 existiert. Gefragt 23 nov 2013 von gast. Nun ist die konvergenz einer reihe nichts anderes als die konvergenz der dazugehörigen partialsummenfolge. Der abstand der folgenglieder wird im verlauf der folge nicht beliebig klein. Juli 2020 um 20:14 uhr bearbeitet. Sei (rn) n2n eine folge in diesem metrischen raum. Das ist ein video im rahmen der playlist analysis i, die äquivalenz zur konvergenz gilt hier, da es um r geht, abe. Also ist die monoton wachsende folge p n n=1 2 na 2n 1 n=1 nach oben beschr ankt und daher. Cauchyfolge), cauchysche folge oder fundamentalfolge ist in der mathematik eine folge, bei der der abstand der folgenglieder im verlauf der. Trotz seines hohen alters ist es zu entziffern und forscher viele geheimnisse des alten orients entdeckt. Cauchyfolge), cauchysche folge oder fundamentalfolge ist in der mathematik eine folge, bei der der abstand der folgenglieder im verlauf der folge beliebig klein wird.
Der abstand der folgenglieder wird im verlauf der folge beliebig klein. • beispiel f¨ur einen unendlichdimensionalen vektorraum. Gefragt 23 nov 2013 von gast. 4 ausgehend von der in lemma 45.10 formulierten alternative: Der beweis zum obigen satz ist ähnlich wie der entsprechende beweis bei konvergenten folgen:
4 ausgehend von der in lemma 45.10 formulierten alternative: Dazu müssen wir zeigen, dass es zu jedem ϵ > 0 {\displaystyle \epsilon >0} ein n ∈ n {\displaystyle n\in \mathbb {n} } gibt, so dass für alle n , m ≥ n. Diese seite wurde zuletzt am 5. Diese beweisrichtung haben wir im obigen beispiel gezeigt. Eine folge (an), die in einem endlichdimensionalen vektorraum v bez¨uglich einer norm k·k in v gegen einen grenzwert a ∈ v konvergiert, konvergiert ebenso bez¨uglich jeder anderen norm k·k′ in v gegen a. Da aber 2 \sqrt 2 2 keine rationale zahl ist, konvergiert sie jedoch nicht in q \dom q q (in r \dom r r würde sie selbstverständlich konvergieren). Der abstand der folgenglieder wird im verlauf der folge nicht beliebig klein. Trotz seines hohen alters ist es zu entziffern und forscher viele geheimnisse des alten orients entdeckt. 📘 siehe beweise im wiki 1 antwort + 0 daumen. Cauchyfolge), cauchysche folge oder fundamentalfolge ist in der mathematik eine folge, bei der der abstand der folgenglieder im verlauf der. Prinzipien und beispiele das babylonische zahlensystem, entstand tausende von jahren vor der christlichen ära war der anfang vom anfang der mathematik. Der abstand der folgenglieder wird im verlauf der folge nicht beliebig klein. (f ur n= 1 wurde das in analysis i gezeigt.
Cauchy Folge Beispiel: Der abstand der folgenglieder wird im verlauf der folge beliebig klein.